Dokumentáció
Megjegyzés: itt nagyrészt technikai részletek vannak leírva a program működésével kapcsolatban. Bár éltem azzal az előfeltételezéssel, hogy az Olvasó rendelkezik a szükséges szakismeretekkel, ennek ellenére igyekeztem több helyen közérthetőbb formában is megfogalmazni a dolgokat.
Tartalomjegyzék
A fejlesztés legelső percétől kezdve az volt a legalapvetőbb szempont, hogy az alkalmazást bárki, ingyen, mindenféle regisztráció nélkül használni tudja.
A fázis-egyensúlyi számítások jellemzően bonyolultak, és sokféle adatra van szükség hozzá. A második alapvetés így az lett, hogy a program a felhasználótól csak a feltétlenül szükséges adatokat kérje, így minél egyszerűbb legyen a használata. A felhasználó a feladata lényegére kell tudjon összpontosítani, ne kelljen számára érdektelen, de a számításokhoz szükséges adatokat vadásznia.
Ennélfogva a program nagyfokú önállóságra "lett nevelve". Rengeteg adatot gyűjtöttem össze, amiből önállóan válogatja le a szükséges dolgokat, az éppen elvárt feladatnak megfelelően - legyen az ábra készítés, folyamat-modellezés, vagy akármi. Sokféle anyag és azok kombinációi vizsgálhatók az alkalmazással, hogy minél szélesebb körű problematikákhoz lehessen használni - akár az oktatásban akár az ipari gyakorlatban.
Még egy szempont volt a fejlesztés során, hogy lehetőleg megbízható is legyen. Az anyagok adatait lehetőség szerint több forrásból vettem, a téves adatokat így ki lehetett szűrni. A program olyan eljárásokkal dolgozik, ami a jelenlegi szakmai igények szerint elvárható pontosságú eredményeket ad. Demonstrációs célra mindenképpen jó, ipari feladatok megoldásához is sokan használják. -- Bár van még hova fejlődni. --
Ez az alkalmazás alapvetően csak a gőz és a folyadék halmazállapot közötti egyensúllyal illetve átmenetettel foglalkozik, a szilárd állapottal nem. Ennek oka is van, mégpedig az, hogy az itt alkalmazott nem-idealitási modellek nem teljesen alkalmasak erre, valamint a szilárd fázisú addíciós vegyületek jóval összetettebb fázisdiagramokat tudnak okozni, mint a folyadék-elegyedési és gőz-folyadék "halgörbék". (Valójában a szilárd adduktok nem jósolhatók azokkal az eszközökkel, amiket a VLE - Calc .com használ.) Ennélfogva a szilárd-folyadék egyensúly (SLE, oldhatóság) egy külön projekt lett. (Fejlesztése átmenetileg szünetel.)
Ugyanakkor a folyadék-folyadék (LLE) és gőz-folyadék egyensúlyokat (VLE) egyaránt, és egyszerre kezeli. Ennek is fontos oka van, valójában csakis így működik jól, együttesen (VLLE). Több-összetevős rendszerek esetén minden VLE számolás előtt megvizsgálja a folyadék-stabilitást (lesz-e két folyadékfázis), ha van akkor pontosan meghatározza a fázisok összetételét, és csak utána, ezen adatok ismeretében vág bele a VLE számolásoknak.
A VLLE számításokat jelenleg két célra használja ez az alkalmazás: különféle fázis-diagramok készítésére, illetve desztilláció modellezésre.
Az adatbázisban kb. 330 vegyület található meg, azonosítókkal, szinonim nevekkel, összegképlettel, alapvető fizikai tulajdonságaival, és a szerkezetüket leíró UNIFAC funkciós csoportokkal. Az anyagok adatait lehetőség szerint több forrásból vettem, a téves adatokat így ki lehetett szűrni.
A fizikai jellemzők:
- mólsúly (g/mol)
- folyadék sűrűség (g/cm3)
- olvadáspont (°C)
- forráspont (°C) légköri nyomáson
- kritikus hőmérséklet (K)
- kritikus nyomás (bar)
- kritikus térfogat (cm3/mol)
- fajhő folyadékban (J/mol⋅K)
- fajhő szilárdon (J/mol⋅K)
- párolgáshő (kJ/mol) *
- olvadáshő (kJ/mol)
- szublimációs hő (kJ/mol)
- Antoine konstansok
- Acentrikus faktor
- Matias-Copeman paraméterek
*
Néhány anyagnál nem találtam a szakirodalomban se Antoine konstanst, se párolgáshőt.
Amennyiben rendelkezésre állt a normál forráspont és egy
gőznyomás adat valamilyen hőmérsékleten (általában szobahőfokon),
úgy ezeknél számítással becsültem meg a párolgáshőt, a Clausius-Clapeyron egyenlettel (ld.
4.1 fejezetben).
Tiszta anyagra (egyetlen vegyületre) általában az Antoine-egyenlettel számoljuk. Ez egy empírikus egyenlet három, az anyagra jellemző konstanssal:
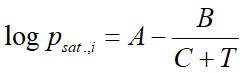
ahol:
- psat.,i az anyag gőznyomása (bar)
- T a hőmérséklet
- A,B,C pedig az Antoine konstansok
A VLE - Calc .com adatbázisában a legtöbb anyagra ezek a konstansok meg is vannak. Amely anyag esetében ezek nincsenek meg, ott a Clausius-Clapeyron egyenlettel számítódik a gőznyomás:
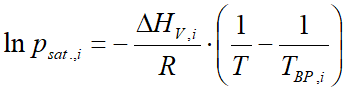
ahol:
- psat.,i az anyag gőznyomása (bar)
- ΔHV,i a párolgáshő (párolgási entalpia) (J/mol)
- R az univerzális gázállandó (8,314 J/mol⋅K)
- T a hőmérséklet (Kelvin)
- TBP a normál forráspont (légköri nyomáson) (Kelvin)
Többkomponensű rendszer esetében, ha a hőmérséklet és a nyomás nincs nagyon közel a kritikus ponthoz (a gőzfázis ideális gáznak tekinthető), a Raoult törvényt használhatjuk, az aktivitási együtthatóval módosítva:
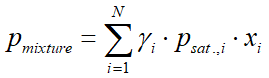

ahol:
- pmixture az elegy gőznyomása (bar)
- γi(gamma) az i-dik komponens aktivitási együtthatója (ld. 4.4 fejezet)
- psat.,i az i-dik komponens gőznyomása (bar)
- xi az i-dik komponens móltörtje a folyadék fázisban
- yi az i-dik komponens móltörtje a gőz fázisban
Vannak anyagok, amelynek molekulái a gőzfázisban asszociátumokat képeznek, és ezért még a módosított Raoult törvénnyel is téves gőz-összetétel adódik. Tipikus példa az ecetsav-víz páros: önmagában a módosított Raoult törvénnyel minimális forrpontú azeotróp adódik, pedig a valóságban ez a rendszer zeotróp. Ilyenkor figyelembe kell venni az asszociációt még alacsony nyomásokon is.
Ennél a programnál J. Gmehling módszerét adoptáltam (ld. 7.fejezet). A módszer lényege, hogy az asszociációt egyensúlyi kémiai reakcióként kezeli.
![ecetsav dimerizáció CH3COOH + CH3COOH <==> [CH3COOH]2](acetic_acid_dimerization.png)
Ehhez az egyensúlyi reakcióhoz hozzárendelünk egy egyensúlyi állandót, ami csak a hőmérséklettől függ:
KD = pi,D / p2i,M
ahol pi,M a monomerek parciális nyomása, pi,D a dimerek parciális nyomása.
A következő egyszerűsítésekkel élünk:
- csak karbonsavaknál foglalkozunk az asszociációval
- csak dimerizációt feltételezünk
- kereszt-dimerizációt (különböző anyagok asszociációját) nem vesszük figyelembe
- minden karbonsav csoportot tartalmazó anyaghoz ugyanazt az egyensúlyi állandót használjuk (nem használunk anyag-specifikus egyensúlyi állandókat)
- (A folyadékfázisú asszociáció az aktivitási együtthatóban fejeződik ki.)
A gőzfázisú dimerizáció számítása az alábbiak szerint megy:
- Kiszámítjuk a dimerizáció egyensúlyi állandóját az adott T hőmérsékleten:
ln KD = AD + (BD / T)
(AD és BD konstansok.)
-
Ezután a dimerizáló komponens(ek)re kiszámítjuk a monomer és dimer specieszek parciális nyomásait:
psat.,i,M = (−1 + √1 + 4⋅KD⋅psat.,i) / 2⋅KD
pi,M = xi ⋅ γi ⋅ psat.,i,M
pi,D = KD ⋅ p2i,M
- A dimerizáló komponens(ek)nél figyelembe kell venni, hogy a dimer 1 molekulának számít
a gőznyomásban, de 2 molekulának számít a gőz-összetételben:
pi = pi,M + pi,D
yi = (pi,M + 2⋅pi,D) / pmixture
Többkomponensű rendszerek számításos modellezéséhez általában szükség van egy "eszközre" (vagy inkább módszerre), amivel a különféle anyagok egymásra hatását figyelembe vesszük. Ennél a programnál az u.n. aktivitási együtthatót (koefficienst) használjuk. (Ez egyfajta mérőszám, hogy egy oldatban az egyes összetevők molekulái milyen erős kölcsönhatásban vannak a többi összetevő molekuláival. Mondjuk úgy is, hogy a "nem-idealitás mértéke".)
A VLE - Calc .com jelenleg a UNIQUAC és a UNIFAC módszert használja. Az előbbi konkrét anyagokhoz használatos, és konkrét kísérleti méréseken alapuló paraméterekkel működik. Az utóbbi egy csoportjárulék módszer, így - elvileg - tetszőleges molekulákra használható, anélkül hogy kísérleti adatokból származó paraméterekkel rendelkeznénk. A UNIFAC - nagyon leegyszerűsítve - úgy működik, hogy az egyes vegyületeket funkciós csoportok összességeként definiálja (kisebb darabokból rakja össze, mint a LEGO), és az egyes csoportok közötti molekuláris kölcsönhatások összességéből számítja ki (elég bonyolult képletek segítségével) az aktivitási együtthatót.
Bizonyos (gyakori) vegyület-párok esetén a UNIFAC prediktív ereje (jóslás pontossága) kifejezetten gyengének mutatkozik, ezért a fejlesztés során néhány vegyület pár esetére kísérleti adatsorokon alapuló UNIQUAC kölcsönhatási paraméterek lettek meghatározva és rögzítve a VLE-Calc.com adatbázisában. Amikor olyan többkomponensű rendszert vizsgálunk a programmal, amely esetében az összes vegyület-párosra megvannak a UNIQUAC paraméterek, ott a program automatice ezeket használja a UNIFAC helyett.
UNIFAC-ból kettő verzió is bekerült a programba. Egyiket akkor használja a program, ha állapot-függvényt kell használnia ("EOS" - lásd következő fejezetben), a másikat meg ha nem.
A UNIFAC elvileg tetszőleges vegyület-kombinációk kezelését lehetővé teszi, a gyakorlatban ez azért így sajnos nem igaz. Bizonyos kombinációkat lehet, másokat nem lehet vele használni. Ez attól függ, hogy az általunk vizsgálandó vegyületekben előforduló funkciós csoportok mindegyikére igaz-e, hogy bármely másik előforduló csoporttal való kölcsönhatást leíró paraméterek rendelkezésre állnak-e. Mert ha nem, akkor a program inkább nem engedi az illető anyagokat egyidőben kiválasztani, nehogy a hiányzó paraméter miatt fals eredményeket közöljön.
Ez a fajta tiltás úgy valósul meg, hogy mielőtt az anyaglistát (vegyület kiválasztáshoz) megjelenítené, előbb megvizsgálja, hogy a már kiválasztott vegyület mely más vegyületekkel párosítható-e, a rendelkezésre álló kölcsönhatási paraméterek tekintetében. Amelyekkel nem mehet, azokat nem jeleníti meg a listán, így kiválasztani sem lehet.
Normál körülmények között (értsd: általános oldószerek, szobahőfok és 100°C között, normál vagy csökkentett nyomáson) a gőznyomás számításokhoz elegendő az u.n. Raoult törvényt (ld 4.2. fejezetben) használni, természetesen módosítva az aktivitási együtthatóval. (A gőzfázis ideális gáznak tekinthető.)
Ám ha a rendszer közel van a kritikus állapothoz (vagy szuperkritikus komponenseket tartalmaz), akkor már szükséges valamiféle állapotfüggvényt használni, mert figyelembe kell venni, hogy a gőzfázis már nem ideális gázként viselkedik.
A VLE - Calc .com jelenleg a PSRK (Predictive Soave-Redlich-Kwong) állapot-függvényt használja. Előnye, hogy az UNIFAC modellt veszi segítségül, így az aktivitási részhez jól illeszthető volt (ld. 4.4 fejezet).
Az állapot-egyenlet (EOS) használatához jópár specifikus adatra van szükség (pl. az anyagok kritikus állandói és egyéb speciális paraméterei). A vegyület-választó lista megjelenítése során a program megvizsgálja, hogy mely anyagokhoz állnak rendelkezésre az EOS-használathoz szükséges az adatok, és a feladattól függően vagy kigyomlálja a listából azokat, amikkel nem lehet EOS-számolást csinálni, vagy tiltja az EOS-használatot, és csak olyan hőmérsékleti/nyomás viszonyok közötti számolást enged, amihez nem kell az EOS.
Adott hőmérséklethez tartozó gőznyomást kiszámolni a 4.2. (Raoult-törvény) szerint aránylag egyszerű. Ennek fordítottja egyetlen anyag esetében még szintén könnyen megoldható (mind az Antoine- mind a Clausius-Clapeyron egyenletek átrendezhetők explicit módon T-re). Több komponensű elegy esetén viszont már korántsem triviális, hogyan lehetséges a T hőmérséklet megtalálása pmix össznyomáshoz.
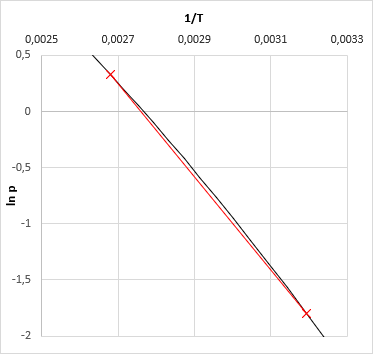
A szakirodalom általában iterációs megoldásokat javasol, mint például a kvázi-Newton szelőmódszer, amit a VLE-Calc.com korai verziói használtak. Ez a program jelenleg egy olyan módszert alkalmaz, ami azon a tényen alapul, hogy az ln(p) − 1/T gőznyomás függvény közel lineáris (még akkor is ha többkomponensű a rendszer), legalábbis nem túl tág hőmérséketi tartományban. Az algoritmus:
- kiszámoljuk az összes komponens forrás-hőmérsékletét a megadott nyomáson
- kiszámoljuk az elegy gőznyomását a legkisebb és a legmagasabb hőmérsékleten
- a két-két nyomás és hőfok adat alapján kiszámítjuk az ln(p) − 1/T egyenes paramétereit (meredekség és tengelymetszet)
- az illesztett egyenes egyenletéből kiszámoljuk a keresett hőmérsékletet a megadott nyomáshoz - ez az elegy buborékpontja ezen a nyomáson.
- A már birtokunkban lévő harmadik hőmérsékletre megint csak kiszámítjuk az elegy gőznyomását. (Ennek tehát már nagyon közel kell lennie a feladat elején megadott nyomásértékhez. Ha mégsem akkor valamit elrontottunk.)
- A 3-3 kiszámolt ln(p) és 1/T értékre most egyenes helyett másodfokú függvényt illesztünk, és arról is leolvassuk a megadott nyomáshoz tartozó hőmérsékletet - ez az elegy buborékpontja ezen a nyomáson.
- (Ha szükségünk van a gőzösszetételre is, akkor még egyszer számolunk elegy gőznyomást, annak "mellékterméke" a gőzösszetétel.)
Megjegyzés: Ez már egy aránylag pontos eredmény (a hibája általában kb. 0,1°C körüli), kevésbé igényes alkalmazásoknál itt meg is lehetne akár állni. Azonban ez az eredmény viszonylag olcsón tovább pontosítható! (Nagyságrendekkel lesz pontosabb.)
Ez a módszer számítástechnikailag olcsó (tehát gyors), fix 4-szer kell elegy gőznyomást számolni a pontos eredmény eléréséhez, míg a secant módszerrel általában ennél többször.
Bevezetés
A különféle folyadékok vagy elegyedenek egymással - vagy nem. (De az biztos.) Persze, odáig rendben, hogy vízzel a szénhidrogének, meg egy csomó más szerves vegyület nem elegyedik... de vannak olyan esetek is szép számmal, melyeknél egyáltalán nem triviális, hogy az elegy szétválik-e vagy nem.
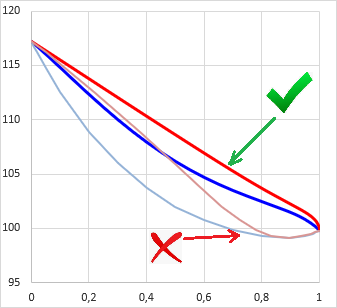
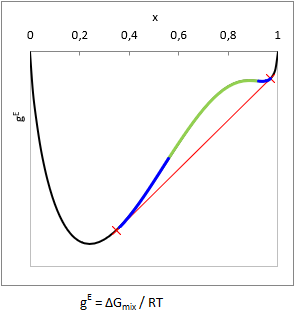
Elméletben megjósolható a szételegyedés a Gibbs elegyítési szabadentalpia függvény (gE = ΔGmix.(x,T)/RT) görbületéből: ha valamely összetételnél az elegyítési szabadentalpia az összetétel függvényében alulról konvex, azaz ∂2gE(x,T)/∂x2 < 0, akkor annál a (bruttó) összetételnél biztosan egynél több folyadékfázis lesz egymással egyensúlyban. Ez az instabil zóna (ld. az ábrán zölddel).
Két komponens esetén a fázisok egyensúlyi összetételét az ábra szerinti érintő megszerkesztésével lehet megállapítani (ld. az ábrán pirossal). Egyensúlyban minden komponens aktivitása (ai=γi⋅xi) azonos mindkét fázisban, ezért számítástechnikailag ekvivalens megoldás az izoaktivitású összetételek megkeresése (ai,1.fázisban = ai,2.fázisban).
A gyakorlatban azonban van egy kicsike probléma a fentiekkel. Vegyük észre az ábrán, hogy a piros érintő fölött a gE függvény nem mindenhol konvex alulról (ld. az ábrán kékkel). Ez az u.n. metastabil zóna. Ha egy olyan bruttó összetételű eleggyel van dolgunk, ami a metastabil zónába esik, a második derivált előjelének vizsgálata nem fogja kimutatni, hogy az elegy két-fázisú.
Három vagy több komponens esetén a helyzet tovább bonyolódik, mert két- vagy több-dimenziós felületeken kell a fenti fogalmakat (zónákat) értelmezni, és numerikusan kezelni. Ennek mikéntje nagyon nem triviális, számos publikáció foglalkozott a témával az elmúlt évtizedekben. A VLE - Calc .com korábbi verziói a fentiekben leírt második derivált vizsgálaton és izoaktivitású pontok keresésén alapuló módszert használtak, ennélfogva nem is mindig érzékelte a rendszer heterogén voltát. De ami sokkal kellemetlenebb, hogy fals egyensúlyi koncentrációkat is produkált időnként, ami azt okozta a LLE-diagramokon, hogy a konódák nem mindig következetesen sorakoztak egymás fölé, sőt voltak egymást keresztezőek is. (Ez utóbbi nem programhiba miatt volt, hanem a termodinamikai modellből adódik - ld. később).
Folyadék stabilitás vizsgálat
A bevezetőben leírt próblémák miatt a VLE - Calc .com jelen verziójához Wasylkievich és munkatársainak módszerét adoptáltam. Ez egy nagyon kifinomult megközelítés, ami megbízhatónak bizonyult - igaz rendkívül nehéz volt reprodukálni és itt implementálni.
A módszer lényege, hogy az úgynevezett Tangent-Plane-Distance-Function (magyarul kb. "Érintő-sík-távolság-függvény", hadd legyen TPDF a továbbiakban) lokális minimumait (vagy inflexióit) keresi meg, és a minimumokból kiindulva kell megkeresni az egyensúlyi összetételt. A módszernek számos előnye van:
- metastabil zónában is kimutatja, ha a rendszer heterogén
- akárhány komponens esetén is használható (elvileg)
- az egyensúlyi összetétel kereséséhez nagyon jó kiinduló pontokat szolgáltat
- azt is képes kimutatni, ha a talált egyensúlyi összetétel esetleg fals
- azt is képes kimutatni, ha a rendszer 2-nél több fázisra ugrik szét (2-nél több komponens esetén lehetséges)
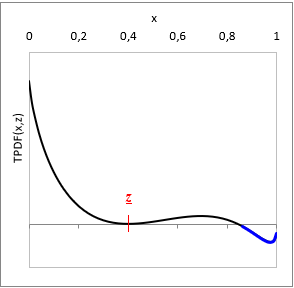
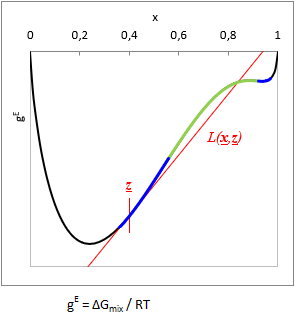
Adott T hőmérsékleten és z bruttó elegy-összetételnél:
TPDF(x) = gE(x) − L(x, z)
ahol L(x, z) a gE-t a z bruttó összetétel pontban érintő függvény.
Ha adott z-nél TPDF(x) bármely x-ben negatív, akkor az elegy nem stabil, bizonyosan több fázisú. (Ld. a TPDF ábráján kékkel)
Két-komponensű rendszerek
Biner elegy esetén a TPDF lokális minimumai (valamint inflexiók, maximum) az összetétel szerinti első deriváltjának zérushelyein vannak. Jelen implementációban a zérushelyeket egy kvázi-Newton módszerrel keressük meg. Méghozzá nem is mindet, hanem azt a kettőt, ami a legvalószínűbben a legközelebb van a TPDF minimumaihoz.
A módszernél kihasználjuk a biner gE függvény néhány hasznos tulajdonságát:
- nincs mindig maximuma, de ha mégis, akkor mindig csak egyetlen maximuma van,
- az összetétel-tér széleitől befelé irányban mindig negatív a meredeksége.
Ezért ha mégis van maximuma, a "szélekről indulva" a keresést, biztosan vagy lokális minimumot, vagy legfeljebb inflexiót találunk. A biner TPDF első deriváltja felírható egy közelítő analitikus deriválttal, és azt a nullával egyenlővé lehet tenni:
∂TPDF(x1,2) / ∂x1 ≅ (ln x1 + ln γ1(x) − ln z1 − ln γ1(z)) − (ln x2 + ln γ2(x) − ln z2 − ln γ2(z)) = 0
Az algoritmus:
- Kiszámítjuk az aktivitási együtthatókat z bruttó összetételnél (γ1,2(z)), eltesszük (konstans az eljárás során).
- Induljunk ki x1=0 pontból ("feltételezett x").
- Kiszámítjuk az aktivitási együtthatókat x-ben (γ1,2(x)).
-
A fenti analitikus deriváltból levezethetők alábbi képletek, amikből az új x adódik:
c1 = ln γ1(x) − ln z1 − ln γ1(z)
c2 = ln γ2(x) − ln z2 − ln γ2(z)
x1,ÚJ = exp (−c1 + ln x2 + c2)
x2,ÚJ = 1 − x1,ÚJ
- Az új x-ekkel ismét kiszámoljuk az aktivitási együtthatókat, és iteráljuk az egészet konvergenciáig. A kapott x az x1=0-hoz legközelebbi minimum vagy inflexió.
- Megismételjük a fenti eljárást x1=1-ből kiindulva is. Ebből lesz a másik lokális minimum vagy inflexió - már ha van. Mert ha csak egyetlen minimum van és nincs inflexió, akkor a két eljárás ugyanarra az eredményre jut, ilyenkor homogén a rendszer.
A kapott x értékeknél eztán megvizsgáljuk, hogy a TPDF negatív értékű-e valamelyiknél. Ha igen, akkor a rendszer instabil (heterogén, 2-fázisú). Ilyenor ezekkel az x értékekkel kiindulva lehet nekiállni megkeresni az egyensúlyi összetételt ("LLE-flash"). Erre a Rachford-Rice egyenletet használjuk (ld. lejjebb).
Három- vagy több-komponensű rendszerek
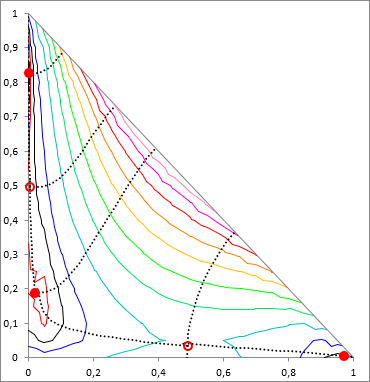
Ahogy a bevezetőben már említésre került, többkomponensű rendszerben a helyzet sokkal bonyolultabb, mint biner esetben. S. Wasylkievich és munkatársainak eljárása viszont nagyon nagy biztonsággal kezeli a helyzetet, akárhány komponens esetében is - ámbár meglehetősen számításigényes. A képletekbe itt már nem mennék bele, a hivatkozott cikkben minden részletesen le van írva.
Az eljárás lényege, hogy n-komponens esetén a TPDF függvény egy (n−1)-dimenziós felület, aminek a minimumait keressük. Ez a felület olyan mint egy "gyűrött rongy", vannak lokális minimumai (teli piros pöttyök az ábrán), lehet rajta lokális maximum, lehetnek nyeregpontok (üres piros pöttyök az ábrán)- ezeket a TPDF stacionárius pontjainak hívjuk, ahol az összes i komponens móltörtje szerinti parciális derivált zérus ( ∂ TPDF(x) / ∂xi = 0). Ezeket a stacionárius pontokat "hegy-gerincek" (ridges) és "völgyek" (valleys) kötik össze. Az eljárás során ezen hegyek és völgyek mentén feltérképezzük az egész (n−1)-dimenziós felületet, és így találjuk meg az összes stacionárius pontot, köztük a minimumokat is.
Amikor a minimumok megvannak, hasonlóan mint a 2‑komponensű esetben itt is megvizsgáljuk őket, hogy a TPDF negatív értékű-e valamelyiknél. Ha igen, akkor a rendszer instabil (heterogén). A lokális minimumokhoz tartozó összetételekből kiindulva lehet nekiállni megkeresni az egyensúlyi összetételeket ("LLE-flash", Rachford-Rice egyenlettel, ld. lejjebb).
Sajnos az így, elsőre talált egyensúlyi összetételek 3- vagy több komponens esetén egyáltalán nem biztos, hogy helyes (valós) eredmények. Előfordul ugyanis, hogy adott z bruttó összetételhez nem egy, hanem több izoaktivitású megoldás is tartozik. Ezek közül az a helyes, amelyek közül a rendszer teljes Gibbs szabad-entalpiája a legalacsonyabb.
Ezért az első körben kapott egyensúlyi fázis-összetételek közül az egyiket stabilitás vizsgálatnak vetjük alá, a fentiek szerint (tehát legyen z = xbármely-fázis). Ha a stabilitás vizsgálat eredménye szerint xbármely-fázis stabil (nincs negatív értékű lokális minimum), akkor a talált egyensúlyi fázisok helyes megoldások. Ha a vizsgálat eredménye instabil (van negatív értékű lokális minimum), akkor a talált lokális minimumokból újra meg kell kísérelni az egyensúlyi összetételek keresését.
A lokális minimumok darab-számából lehet következtetni rá, hogy hány folyadék fázisra oszlik szét az elegy, de ez nem jelent garanciát is rá, hogy ténylegesen annyi. Ha pl. három minimum van, akkor érdemes ezt feltételezni, és akkor három egyensúlyi fázist keresni a minimumok alapján. Ha mégsem három fázis lenne, az vagy a Rachford-Rice számításoknál derül ki (automatikusan 2-fázisúra redukálódik a rendszer), vagy a talált fázisösszetételek stabilitásvizsgálatánál.
A Rachford-Rice egyenlet
Amikor már ismert, hogy a rendszer heterogén, meg kell keresni a különböző folyadék-fázisok pontos összetételét. Egyensúlyban az egyes komponensek aktivitása (ai=γi⋅xi) azonos az összes folyadék-fázisban. Ugyanakkor azt is figyelembe kell venni, hogy az egyes komponensek mennyisége a fázisokban együttesen ugyanannyinak kell lennie, mint a bruttó elegyben (anyagmérleg), amit a feladat elején megadtunk (z). Erre Rachford és Rice levezettek egy nagyon hasznos kis egyenletet, melynek megoldásával egyszerre mindkét elvárásnak megfelelő eredményt kaphatunk:
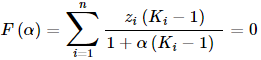
- F(α) az u.n. cél-függvény, a feladat során azt kell elérni, hogy ez nulla értéket vegyen föl
- α egy 0 és 1 közötti szám, azt méri, hogy 1 mol bruttó elegy ha szétválik, hány mol lesz az egyik fázis mennyisége. (A másik fázis meg értelemszerűen 1−α lesz.)
- zi a bruttó elegy i-dik komponensének moltörtje
- Ki az i-dik komponens megoszlási hányadosa a két fázis között: Ki = xi,1.fázis/xi,2.fázis = γi,2.fázis/γi,1.fázis
A Rachford-Rice egyenlet megoldása iteratív úton lehetséges:
- Első lépésben vesszük a stabilitás-vizsgálat során kapott összetételeket és aktiviási együtthatókat, és kiszámítjuk a Ki-ket.
- Meghatározzuk α-t Newton-Raphson-módszerrel. Ehhez behelyettesítünk mindent F(α)-be és annak α szerinti első deriváltjába, és a következő képlettel kapjuk α következő közelítését: αúj = αelőző − F(αelőző) / F'(αelőző). Ezzel az új α-val megismételjük a számításokat, iterálunk konvergenciáig.
- Kiszámítjuk a fázisok összetételeit ezekkel a képletekkel:
xi,1.fázis = zi / (1 + α(Ki − 1))
xi,2.fázis = xi,1.fázis ⋅ Ki - Normalizáljuk a kapott móltörteket (összes fázisnál): xi = xi / ∑nj=1 xj
- A kapott móltörteknél aktivitási együtthatókat számolunk, melyekkel újra kiszámoljuk a Ki-ket, és ismételjük a folyamatot az elejétől kezdve. Iterálunk konvergenciáig.
Kontúr-vonalas forrpont/gőznyomás térkép
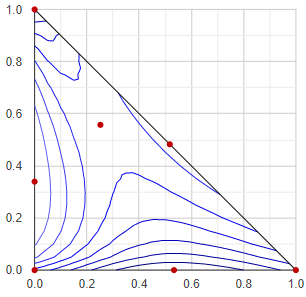
Talán nem a leghasznosabb ábrázolás-mód, de ezt sikerült legrégebben összehoznom, mivel aránylag egyszerű és gyorsan előáll. Lényegében a háromkomponensű elegy forrpontját (buborékpontját - izobár esetben) vagy gőznyomását (izoterm esetben) ábrázolja szintvonalakkal. Hátránya, hogy a gőzösszetétel - mint információ - nem jelenik meg semmilyen formában ebben az ábrázolásmódban.
Az eljárás során a háromszögletű összetétel-teret 20x20-as felbontásban sok kis háromszögre bontjuk, és minden kis háromszög minden sarokpontjában elvégződik egy-egy VLE-számolás. Ezután az összes eredmény közül megkeressük a legkisebb és a legnagyobb hőmérséklet vagy gőznyomás értéket, és ezek között kiválasztunk 8-at a 8 szintvonalnak. Ezek lesznek a "konstans-értékek", mert a kontúrvonalak mentén ezek az értékek állandók. Mindegyik konstans értékkel végig-vizsgáljuk az összes kis háromszöget, hogy ez az adott érték megjelenhet-e benne: ha a háromszög sarkain lévő legkisebb és legmagasabb hőfok/nyomás értékek közé esik a konstansunk, akkor az adott kis háromszögön átmegy a konstans-érték kontúrvonala. Ezután lineáris interpolációval kiszámítjuk, hogy a háromszög élein hol megy át a kontúrvonal, és a háromszöget átszelő szakaszt eltároljuk.
Az összes szakaszt ábrázolva rajzolódnak ki a szintvonalak.
Maradék-görbe térkép
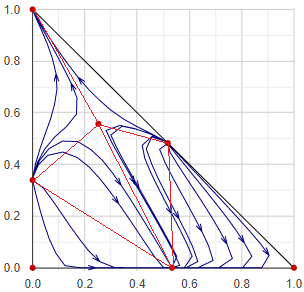
Desztillációs feladatok vizsgálatánál a maradék-görbe ábrázolásmód jóval hasznosabb a forrpont-térképnél. A maradék-görbe azon nyomvonal mentén rajzolódik ki, ahogy egy adott pontból elkezdett szakaszos desztilláció üstmaradékának összetétele változik. Értelemszerűen az illékonyabb régiók felől a kevésbé illékony régiók felé tart, és a görbe irányát minden pontban az adott pontra jellemző egyensúlyi x − y vektor határozza meg.
A maradékgörbe diagramok nagyon sokféle alakúak lehetnek. Valójában az adott terner rendszerben megjelenő azeotróp pontok alapvetően meghatározzák az ábra alakját. Az azeotrop pontok (kiegészítve az egész háromszögdiagram sarokpontjaival, amik a tiszta komponenseket reprezentálják) kisebb tartományokra osztják a teljes összetétel teret. Egy egyszerű, szakaszos desztillációs folyamat alapvetően abban a tartományokban működhet, amelyikbe a kiinudló üst-összetétel esik. Így a maradékgörbe-sereg segítségével könnyedén megállapítható szemrevételezássel, hogy egy adott szétválasztás lehetséges-e, vagy sem.
Az eljárás során először megkeressük a rendszer azeotrop pontjait, ezeket kiegészítjük az egész háromszögdiagram sarokpontjaival - ezeket a pontokat a továbbiakban csomópontoknak hívjuk. A csomópontok halmazát háromszögekbe rendezzük Delaunay-háromszögesítéssel. Minden kis háromszögön belül egy vagy több pontból kiindulva maradékgörbéket generálunk.
A maradékgörbe generálása során a kiinduló pontból először x → y irányban, majd x ← y irányban végig pásztázzuk a kis háromszög tartományát, amíg egy csomóponthoz nem érkezünk. Ekkor választunk egy másik kiindulópontot, és ismét pásztázunk.
Folyadék-elegyedési fázis-diagram
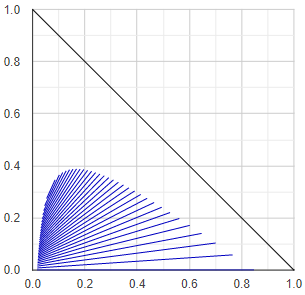
A folyadék-folyadék-egyensúlyi diagramoknak számos fajtája, típusa van. Itt ezekre most nem térnék ki, csak az ábra elkészítésének mikétjére.
A program első lépésben a háromszögdiagram élein lévő biner alrendszereket vizsgálja meg, hogy szételegyedik-e. Amelyik biner alrendszer heterogénnek bizonyul, úgy egyrészt eltárolja az egyensúlyi fázis-összetételeket, másrészt a két fázis pontjai közötti vonal (szételegyedési hézag, angol irodalomban miscibility gap) közepén lévő pontot eltárolja kiinduló pontként.
Ezután a kiiduló pontokból kis lépésközökkel elindul a háromszög belseje felé, és meghatározza a terner szételegyedési húrokat (tie-line, konódák). Az irányt a húr meredeksége szabja meg (mindig a húrra merőleges irányban haladunk tovább), a lépésközt meg a húr mérete - minél kisebb húrok következnek, annál kisebb lépésközzel haladunk tovább. (Ezek a szabályok alapvetően esztétikai célokat szolgálnak.)
Ha menet közben három-fázisú régióba érkezik az algoritmus, úgy a három fázis összetételei által alkotott háromszög további két éleinek közepéről folytatja a lépegetést. Végül az összes kapott húrt felrajzolja diagramba.
Ha terner gőz-folyadék-egyensúly (VLE) számítást végezne a program, előzetesen a fenti algoritmussal előre meghatározza a folyadék-folyadék egyensúlyi húrokat, ezeket eltárolja, és vékony háromszögekbe rendezi. Mielőtt a VLE számolásnak nekiesne, megvizsgálja hogy a megadott folyadék-összetétel beleesik-e valamelyik LLE-háromszögbe. Ha igen, akkor egy egyszerűsített eljárásban meghatározza a szétvált folyadékfázisok összetételét, és azokkal végzi el a VLE-számolást. (Erre az előre kiszámolós-eltárolós dologra azért van szükség, mert a folyadékstabilitás vizsgálat nagyon erőforrásigényes. Kevesebb stabilitás vizsgálatra van szükség ha egy LLE-diagramnyit kell elvégezni, mintha egy desztillálásnyi alkalommal végzi el a program.)
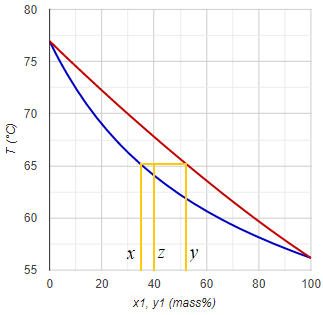
Egyfokozatú folyamatos egyensúlyi desztilláció során a kiinduló folyadékelegyet (betáp) a bepárló készülékben részlegesen párologtatjuk el. A fej- és fenéktermék összetétele az elpárologtatott hányadtól függ. Teljes párlat-elvétel esetén (nincs üstmaradék elvezetve) a párlat összetétele megegyezik a kiinduló elegyével. Ha meg párlat-elvétel nincs, akkor értelemszerűen a fenéktermék lesz azonos a kiindulóval. A köztes helyzet számítása (ami a valóságban általában lenni szokott) a Rachford-Rice egyenlet megoldásával lehetséges (a folyadék-folyadék egyensúlyi számításhoz hasonlóan). (Ezt a fajta számítást az angol nyelvű irodalomban VLE-flash kifejezéssel említik.)
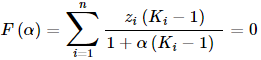
ahol
- F(α) az u.n. cél-függvény, a feladat során azt kell elérni, hogy ez nulla értéket vegyen föl
- α az elpárologtatott hányad, egy 0 és 1 közötti szám, azt méri, hogy 1 mol elegy részleges elpárologtatása során hány mol lesz a gőzfázis mennyisége. (Az elvezetett üstmaradék (a folyadékfázis) meg értelemszerűen 1−α lesz.)
- zi a kiinduló elegy i-dik komponensének moltörtje
- Ki az i-dik komponens megoszlási hányadosa a gőz- és a maradék folyadékfázis között: Ki = yi/xi
A Rachford-Rice egyenlet megoldása iteratív úton lehetséges:
- Az elpárologtatott hányad, az α adott, konstans.
- Első lépésben végzünk egy buborékpont számítást a kiinduló z összetétellel.
- A kapott y-ok segítségével kiszámítjuk (kezdeti becslésként) a megoszlási hányadosokat: Ki = yi/zi
- Kiszámítjuk a fej- és fenéktermék összetételeit ezekkel a képletekkel:
xi = zi / (1 + α(Ki − 1))
yi = xi ⋅ Ki -
Normalizáljuk a kapott móltörteket:
xi = xi / ∑nj=1 xj
yi = yi / ∑nj=1 yj - A kapott x folyadék összetételnél újra buborékpont számítást végzünk, és a kapott új y-okkal újra kiszámoljuk a megoszlási hányadosokat (Ki = yi/xi), és ismételjük (iteráljuk) konvergenciáig.
A szakaszos desztilláció időbeli folyamat, azaz mind az üst-, mind a párlat összetétele időben változik. Ennek modellezéséhez a teljes folyamatot n egyenlő részre kell osztani. A VLE-Calc.com esetében a felbontás n = 200 minden esetben. Akkor is ha ennél kisebb felbontást adunk meg az űrlapon, magát a számítást a háttérben 200 részre osztva végzi, csak ebből annyit rak ki a táblázatba amennyit megadtunk. A program a számításokat mindig mol egységben végzi.
Adott a kezdeti x lepárlandó elegy összetétele. A kiinduló üst mennyiségét a fentiek szerint mindig n = 200 mol (mert így egyszerűbb lett a programkód), ez természetesen a végén átszámítódik a felhasználó által megadott mennyiségnek (és mértékegységnek) megfelelően. Tehát x-ből buborékpont számítást végzünk, és a kapott y gőzösszetétellel számítható, hogy az első dn = 1 mol kipárolt mennyiséggel az üstből melyik komponensből mennyi fogyott:
núj = nrégi − dn
xi,új = (xi,régi ⋅ nrégi − yi ⋅ dn) / núj
A kapott új üst-összetételt eltároljuk, majd ebből indulva megint kiszámoljuk a gőzösszetételt, és így tovább iterálunk, amíg el nem fogy az üstből minden.
A fizikai-kémiai modellek általában mólokkal és móltörtekkel operálnak, de az ember a gyakorlatban legtöbbször tömegben és térfogatban tud gondolkodni.
Egyik fajta feladathoz °C-ban célszerű a hőmérsékletet mérni, másik feladatban Kelvinben. Célszerűnek mutatkozott egy kényelmes
instant mértékegység átváltót beépíteni. Ebben a fejezetben a mértékegység átszámítási módszereket, képleteket lehet tanulmányozni.
Alapvető működés
Jelenleg kilenc mennyiség fajtát kezel a mértékegység-átváltó, noha ebből néhánynak - egyelőre - csak 1-féle mértékegysége van beépítve (magyarul nem váltható át semmilyen más egységbe). Mindegyik mennyiség fajtának van egy alapértelmezett mértékegysége, a program az átváltható numerikus értékeket mindig ebben az egységben tárolja (ezzel végzi a számításokat), és a megjelenítéskor mindig ebből váltja át az űrlapon kiválasztott egységbe.
Az átváltható mennyiség fajták az alábbiak, a jelenleg használható mértékegységekkel:
| Menyiség fajta | Alap egység | További választható egységek |
| Móltömeg | g/mol | - |
| Folyadék sűrűség | g/cm3 | - |
| Hőmérséklet | K (Kelvin) | °C (Celsius), °F (Fahrenheit) |
| Nyomás | bar | kPa, atm, Hg mm, psi |
| Moláris térfogat | cm3/mol | dm3/mol, m3/mol |
| Fajlagos hőkapacitás | kJ/kg⋅K | J/mol⋅K, kCal/kg⋅K, Cal/mol⋅K |
| Látens hő | kJ/mol | kJ/kg, kCal/mol, kCal/kg |
| Koncentráció ill. összetétel | móltört (x) | tömeg%, térfogat%, mol/dm3, g/100 cm3 |
| Anyagmennyiség | kg | g, t, dm3, cm3, m3, mol, mmol, kmol |
Hőmérséklet átváltás
| [K] | = | [°C] + 273,16 |
| [K] | = | ([°F] + 459,688) / 1,8 |
| [°C] | = | [K] − 273,16 |
| [°C] | = | ([°F] − 32) / 1,8 |
| [°F] | = | 1,8 ⋅ [K] − 459,688 |
| [°F] | = | 1,8 ⋅ [°C] + 32 |
Nyomás átváltás
| [bar] | [kPa] | [atm] | [Hg mm] | [psi] | ||
| [bar] | = | n.a | /100 | ⋅1,01325 | /750,0617 | /14,5037738007 |
| [kPa] | = | ⋅ 100 | n.a | ⋅101,325 | /7,500617 | /1450,37738007 |
| [atm] | = | /1,010325 | /101,325 | n.a | /760 | /14,6959488 |
| [Hg mm] | = | ⋅ 750,0617 | ⋅ 7,500617 | ⋅ 760 | n.a | ⋅ 51,71493367 |
| [psi] | = | ⋅ 14,5037738007 | ⋅ 0,145037738007 | ⋅ 14,6959488 | /51,71493367 | n.a |
Fajhő átváltás
| [kJ/kg⋅K] | [J/mol⋅K] | [kCal/kg⋅K] | [Cal/mol⋅K] | ||
| [kJ/kg⋅K] | = | n.a | / M | / 4,1868 | /(4,1868⋅M) |
| [J/mol⋅K] | = | ⋅ M | n.a | ⋅ M /4,1868 | /4,1868 |
| [kCal/kg⋅K] | = | ⋅ 4,1868 | ⋅ 4,1868 / M | n.a | / M |
| [Cal/mol⋅K] | = | ⋅ 4,1868⋅M | ⋅ 4,1868 | ⋅ M | n.a |
ahol M az anyag móltömege.
Látenshő átváltás
| [kJ/mol] | [kJ/kg] | [kCal/mol] | [kCal/kg] | ||
| [kJ/mol] | = | n.a | ⋅ 1000 ⋅ M | / 4,1868 | ⋅ 1000 ⋅ M / 4,1868 |
| [kJ/kg] | = | ⋅ 1000 / M | n.a | /(4,1868⋅M) | /4,1868 |
| [kCal/mol] | = | ⋅ 4,1868 | ⋅ 4,1868 ⋅ M | n.a | ⋅ M |
| [kCal/kg] | = | ⋅ 4,1868 / (1000⋅M) | ⋅ 4,1868 | / (1000⋅M) | n.a |
ahol M az anyag móltömege.
Koncentráció / összetétel átváltás
A különféle koncentráció típusok átváltása kissé bonyolultabb, mint más, egyszerűbb átváltások, mivel a komponensek néhány fizikai adata is szükséges az átszámításhoz.
| [móltört] (x) | [tömeg%] (w) | [térfogat%] (v) | [mol/dm3] (c) | [g/100 cm3] (ρ) | ||
| xi | = | n.a | wi Mi ⋅ ∑nj=1 (wj / Mj) |
vi⋅di Mi ⋅ ∑nj=1 (vj⋅dj / Mj) |
ci ∑nj=1 cj |
ρi Mi ⋅ ∑nj=1 (ρj / Mj) |
| wi | = | 100% ⋅ xi ⋅ Mi ∑nj=1 (xj ⋅ Mj) |
n.a | 100% ⋅ vi ⋅ di ∑nj=1 (vj ⋅ dj) |
100% ⋅ ci ⋅ Mi ∑nj=1 (cj ⋅ Mj) |
100% ⋅ ρi ∑nj=1 ρj |
| vi | = | xi⋅Mi di ⋅ ∑nj=1 (xj⋅Mj / dj) |
wi di ⋅ ∑nj=1 (wj / dj) |
n.a | ci⋅Mi di ⋅ ∑nj=1 (cj⋅Mj / dj) |
ρi di ⋅ ∑nj=1 (ρj / dj) |
| ci | = | 1000 ⋅ xi ∑nj=1 (xj ⋅ Mj / dj) |
1000 ⋅ wi Mi ⋅ ∑nj=1 (wj / dj) |
1000 ⋅ vi⋅di Mi ⋅ 100% |
n.a | 1000 ⋅ ρi Mi ⋅ 100 |
| ρi | = | 100 ⋅ xi ⋅ Mi ∑nj=1 (xj ⋅ Mj / dj) |
100 ⋅ wi ∑nj=1 (wj / dj) |
100 ⋅ vi ⋅ di 100% |
100 ⋅ ci ⋅ Mi 1000 |
n.a |
ahol Mi az i-dik komponens móltömege, és di pedig a folyadék-sűrűsége.
Fontos megjegyezni, hogy a térfogatra vonatkoztatott mennyiségek a fenti módon számolva biztosan nem pontosak. Egyrészt az u.n. térfogat-kontrakció jelensége miatt, másrészt a sűrűség hőmérséklet-függése miatt, amiket ezek a képletek nem vesznek figyelembe. Az eltérés nagyságrendje max. néhány rel.% körüli lehet.
Új ábrák
A VLE-Calc.com számítási lehetőségei további hasznos ábrák készítését is lehetővé teszi, valamint a meglévők kibővítése is a tervek között szerepel. Néhány, a teljesség igénye nélkül:
- p-T fázisdiagram többkomponensű elegyekre ("phase envelope" ábra)
- p-V fázisdiagram többkomponensű elegyekre
- azeotrop összetétel a nyomás függvényében
- desztilláció lefutását (párlat/üstmaradék összetétel változását) szemléltető ábra
- háromszög VLE-diagramokra LLE-diagram montírozás
Új funkciók
A kényelmesebb használat, illetve a még több területen való használhatóság érdekében jelentős fejlesztések, bővítések vannak szintén a tarsolyban, ugyancsak a teljesség igénye nélkül:
- 3-nál több komponensű elegyek kezelése
- rektifikálás (frakciónált desztilláció) számítás
- desztilláció számításnál elő/utó frakciók tervezése, átlagösszetétel meghatározás
- csoportjárulék módszerek bevezetése tiszta anyag fizikai tulajdonságaiak jóslásához
- elegyek fizikai tulajdonságaiak jóslása
- anyagok hőmérsékletfüggő fizikai tulajdonságainak kiszámítása megadott hőfokon
- további vegyületek felvétele az anyaglistába
- tetszőleges anyag használatának lehetősége
Ismert hibák és hiányosságok
Sajnos a jelenlegi program verzió új programhibákat is hozott magával. Az indulás óta számos hibára derült fény (köszönet mindenkinek a visszajelzésekért!), és amit gyorsan ki lehetett javítani, az ki is lett javítva.
Sajnos van egy nagyon makacs, rejtett hiba - vagy inkább működési rendellenesség - amit eddig nem sikerült kiküszöbölni. A leggyakrabban akkor jelentkezik, amikor egy 3-komponensű, heterogén rendszerrel kell VLE-számolást végeznie a programnak, és olykor hibaüzenettel leáll. A leállás valószínűbb, ha az egyensúlyi folyadék-folyadék (LLE) összetételek közt nagyon kis koncentrációk vannak. A hibás működés okát nagyjából sikerült körülhatárolni, de megnyugtató megoldást eddig nem sikerült találni.
Egy másik bosszantó újdonság, hogy az új LLE-eljárás (az új folyadék-stabilitás-vizsgálat) nagyon számítás-igényes, még a mai gyors számítógépeken is elég lassú. (Cserébe megbízhatóbb és többet is tud mint a régi.) A célok között szerepel ezen is változtatni.
Kitekintés
Számos projekt fut párhuzamosan, illetve van betervezve, amelyek többé-kevésbé hasonlóak a VLE-Calc.com-hoz, de más területen használhatók. Ilyen pl. a szilárd anyagok oldhatóságával foglalkozó solubility.info, vagy a már önálló domain-re költöztetett azeotrope.info.
Azok számára, akik a VLE-Calc.com letölthető változata felől érdeklődtek az elmúlt években (ami nincs), érdekes és jó hír lehet, hogy folyamatban van egy Excelben használható verzió készítése. A fejlesztés nagyja már lezárult, a termék nagyrészt készen van, tesztelés és hibajavítások zajlanak. Tervezett közzététel 2021-ben.
Számítási módszerek
-
A. Fredenslund, R.L. Jones, J.M. Prausnitz: Group-contribution estimation of activity coefficients in nonideal liquid mixtures, AIChE Journal, Vol. 21, No. 6, 1975, page 1086-1999
(DOI: 10.1002/aic.690210607)
-
J. Gmehling, J. Li, M. Schiller: Modified UNIFAC model. 2. Present parameter matrix and results for different thermodynamic properties, Ind. Eng. Chem. Res. 1993, 32, 178-193
(DOI: 10.1021/ie00013a024)
-
S. Horstmann, A. Jabłoniec, J. Krafczyk, K. Fischer, J. Gmehling: PSRK group contribution equation of state: comprehensive revision and extension IV, including critical constants and alfa-function parameters for 1000 components, Fluid Phase Equilibria 227 (2005) 157–164
(DOI: 10.1016/0378-3812(91)85038-V)
-
Stanislaw K. Wasylkiewicz et al: Global Stability Analysis and calculation of LLE in multicomponent mixtures, Ind. Eng. Chem. Res. 1996, 35, 1395-1408
(DOI: 10.1021/ie950049r)
- J. Gmehling et al.: Vapor-Liquid Equilibrium Data Collection series, 1981 Dechema
Aktivitási együttható
Állapotegyenlet
Folyadék-stabilitás vizsgálat (LLE)
Gőz-fázisú dimerizáció
Anyag adatok
- E.W. Flick: Industrial Solvents Handbook, 5th ed., 1998 William Andrew Publishing/Noyes
(eBook ISBN: 9780815518099)
- NIST Chemistry Webbook
- Wikipedia
- R. H. Perry, Don W. Green: Perry's Chemical Engineers' Handbook, 1999 McGraw-Hill Inc.
-
Jr. W. Acree, J. S. Chickos: Phase Transition Enthalpy Measurements of Organic and Organometallic Compounds. Sublimation, Vaporization and Fusion Enthalpies From 1880 to 2010, J. Phys. Chem. Ref. Data, Vol. 39, No. 4, 2010
(DOI: 10.1063/1.3309507)
- I. Mellan: Source Book of Industrial solvents, vol.II. (Halogenated hydrocarbons), Reinhold Publishing Corp., N.Y., 1957
- ChemSpider
- Sigma-Aldrich catalog
-
B. E. Poling, J. M. Prausnitz, J. P. O'Connell: The Properties of gases and liquids, 5th ed., McGraw-Hill, 2001
(DOI: 10.1021/ja0048634)
-
P. Martins, P. Sbaite, C. Benites, M. Maciel: Thermal Characterization of Orange, Lemongrass, and Basil Essential Oils; School of Chemical Engineering, University of Campinas (UNICAMP), 13083-970, Campinas –SP, Brazil
(DOI: 10.3303/CET1124078)
- PubChem
-
S. Horstmann, A. Jabłoniec, J. Krafczyk, K. Fischer, J. Gmehling: PSRK group contribution equation of state: comprehensive revision and extension IV, including critical constants and alfa-function parameters for 1000 components, Fluid Phase Equilibria 227 (2005) 157–164
(DOI: 10.1016/0378-3812(91)85038-V)
-
N. N. Greenwood, A. Earnshaw: Chemistry of elements, Second edition, Butterworth-Heinemann, © Reed Educational and Professional Publishing Ltd 1984, 1997
(eBook ISBN: 9780080501093)

